Examples¶
Sometimes the best way to learn an API is by going over some examples. In the folowing ones, it is shown how to model different types of problems and how to solve them.
Unconstrained nonlinear¶
The Rastring function
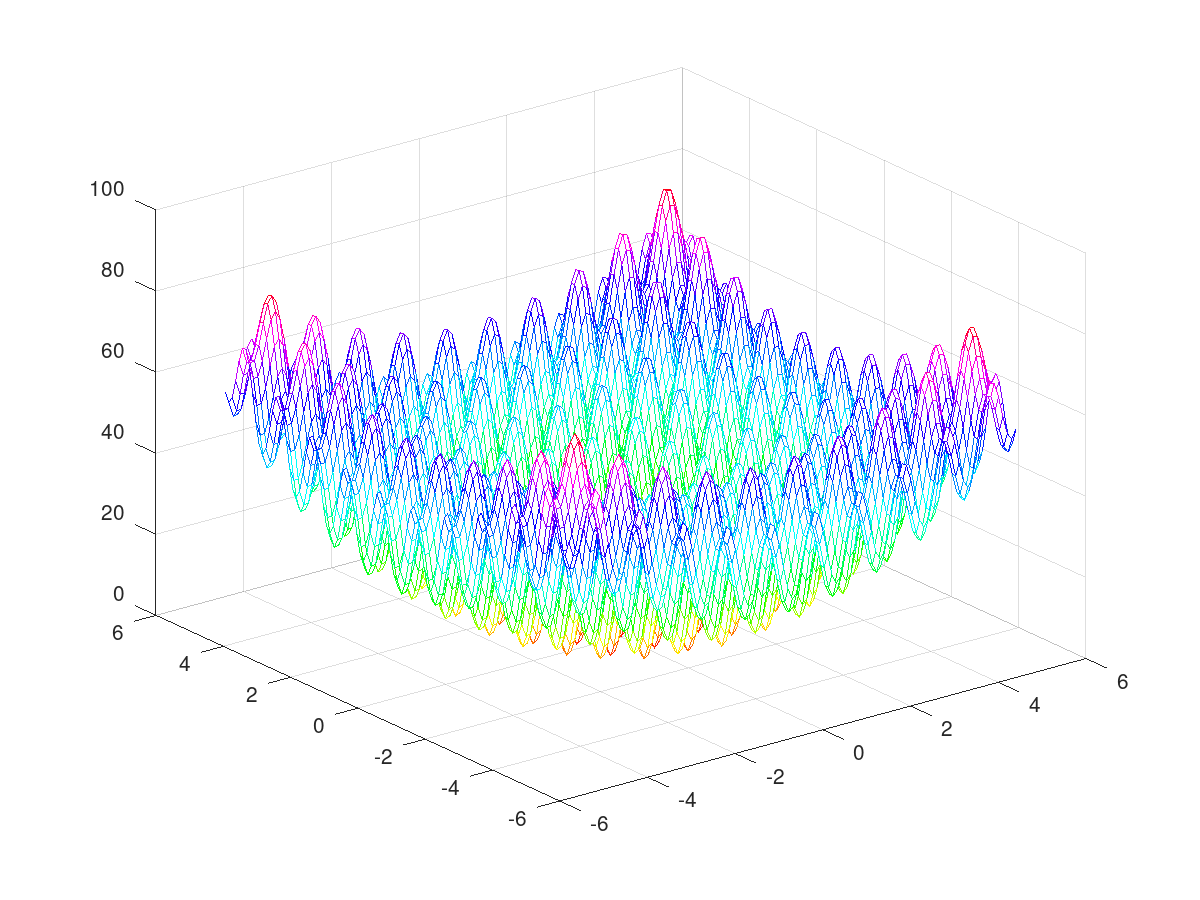
|
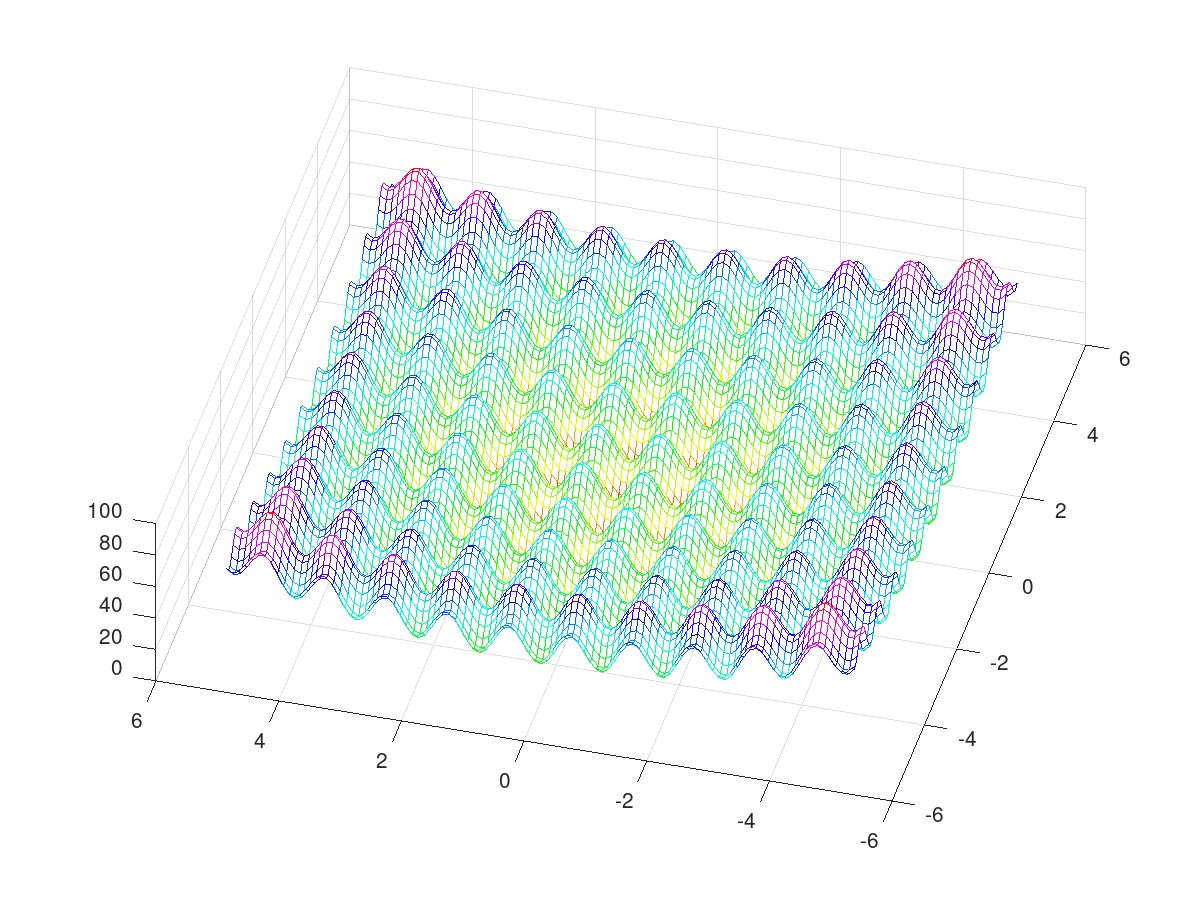
|
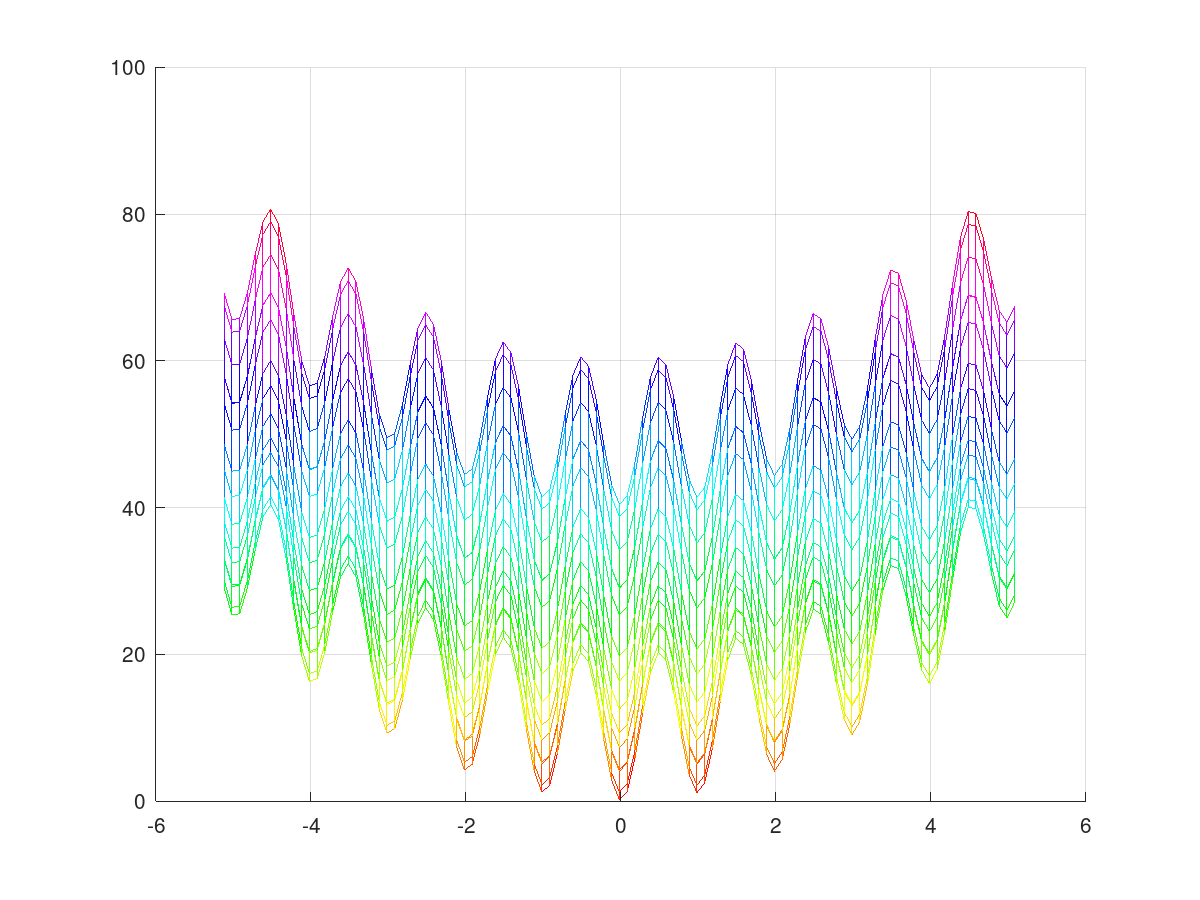
|
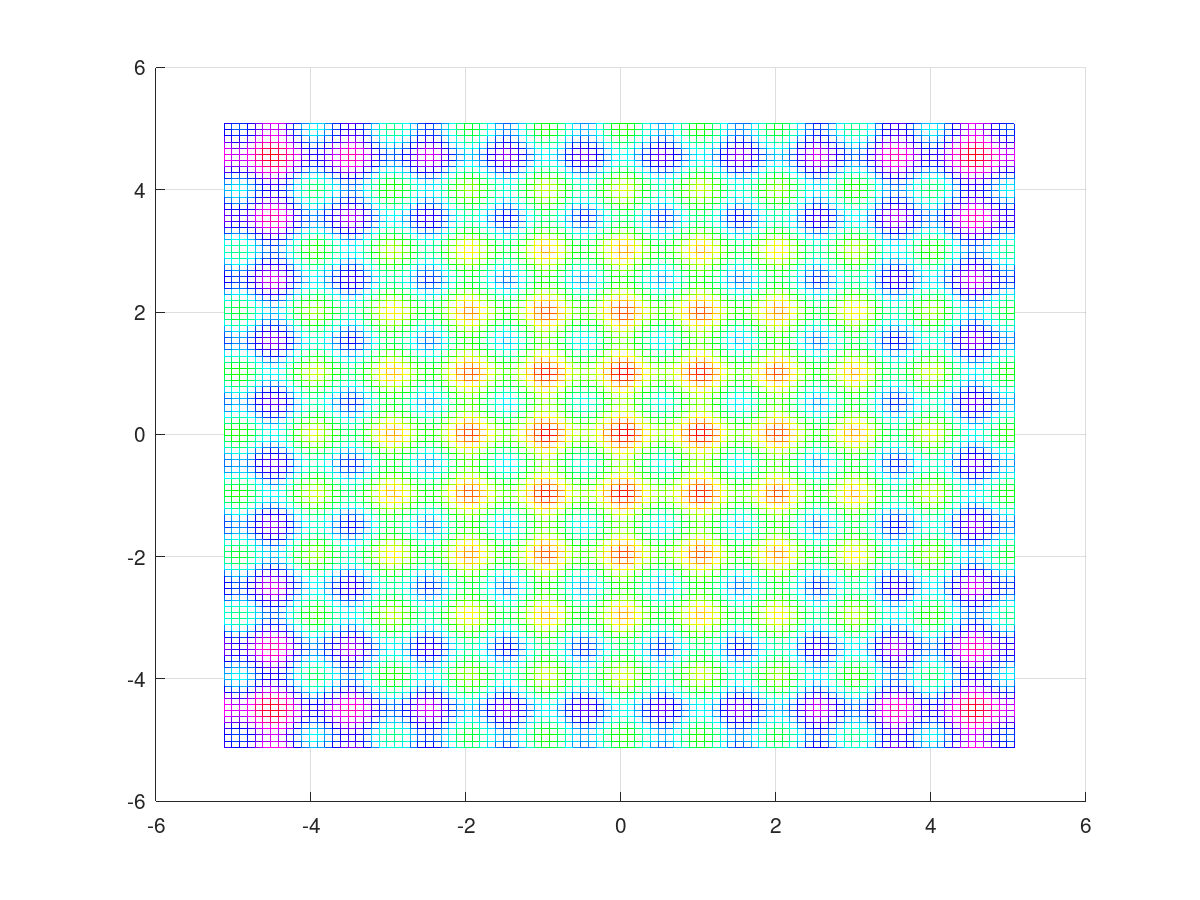
|
import math
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
# Create the model
model = mdl.Model("Rastring")
# Add the variables
x = mdl.Variable(model, "x", lb=-5.12, ub=5.12)
y = mdl.Variable(model, "y", lb=-5.12, ub=5.12)
# Add the objective function
mdl.Minimize(model, "objective", 20 + (x**2-10*mdl.cos(2*math.pi*x)) +
(y**2-10*mdl.cos(2*math.pi*y)))
# Configure the parameters and environment
parameters = mdl.Parameters(objective_goal=1e-7)
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, parameters, environment)
# Print the solution
print(ans.solution)
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 15928375656584496bbb86b3202cd94cef283f8b48f14edd1
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|15928375656584496bbb86b3202cd94cef283f8b48f14edd1|20200622T10:52:45|created: ''
INFO:eut.peerless.solver:..|15928375656584496bbb86b3202cd94cef283f8b48f14edd1|20200622T10:52:49|executed: 'Objective: 0.0. Feasibility: 0.0. Iterations: 0. Elapsed: 0.000396999996'
{x: 0.0, y: 0.0}
Notice the use of the eut.peerless.model.cos function.
The Rosenbrock function
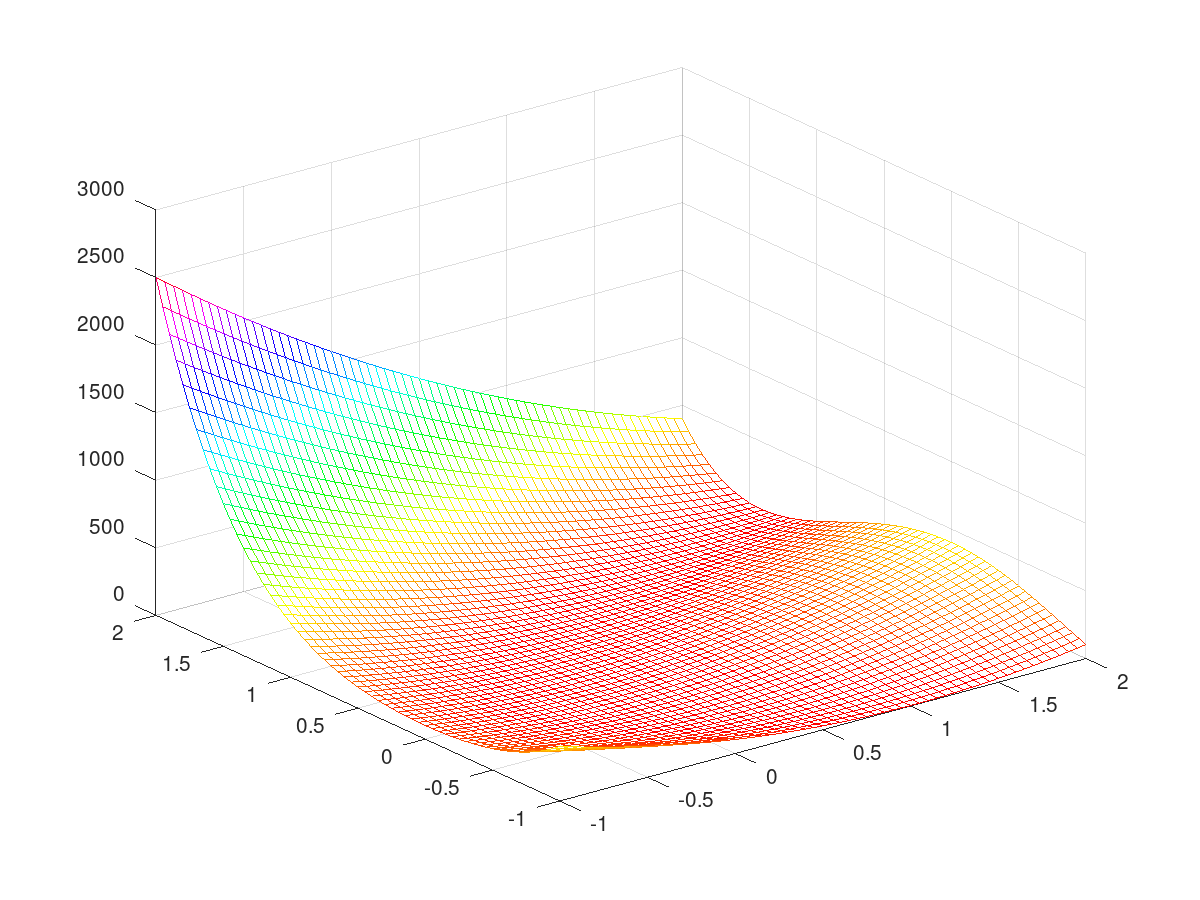
|
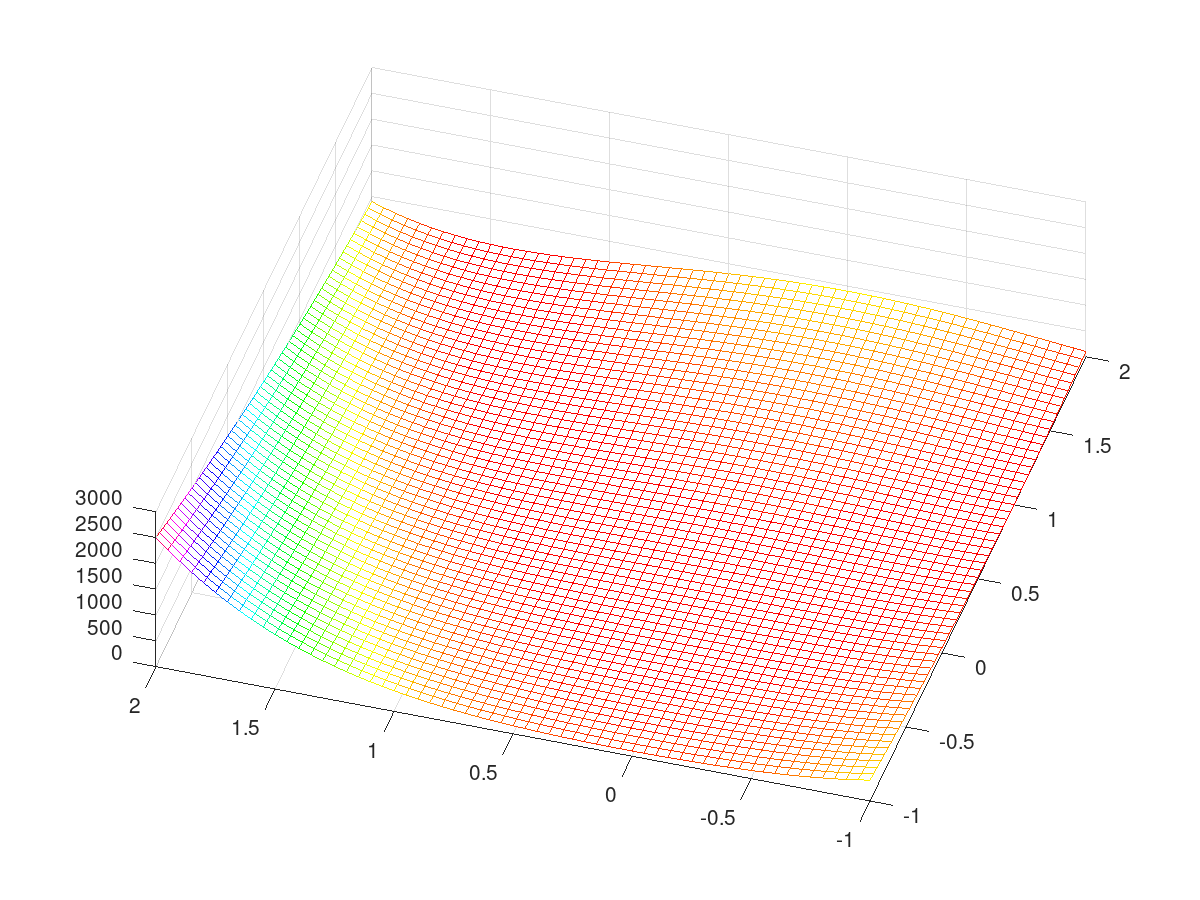
|
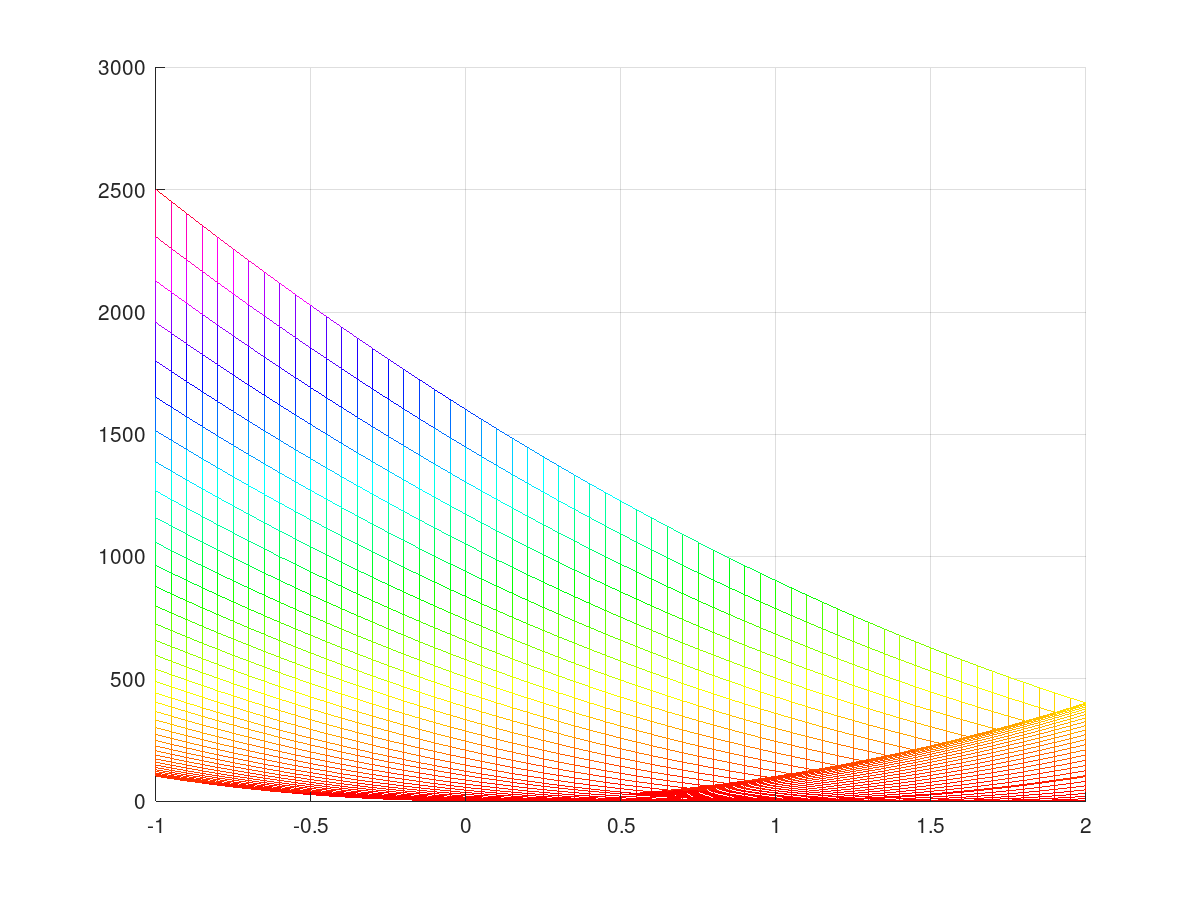
|
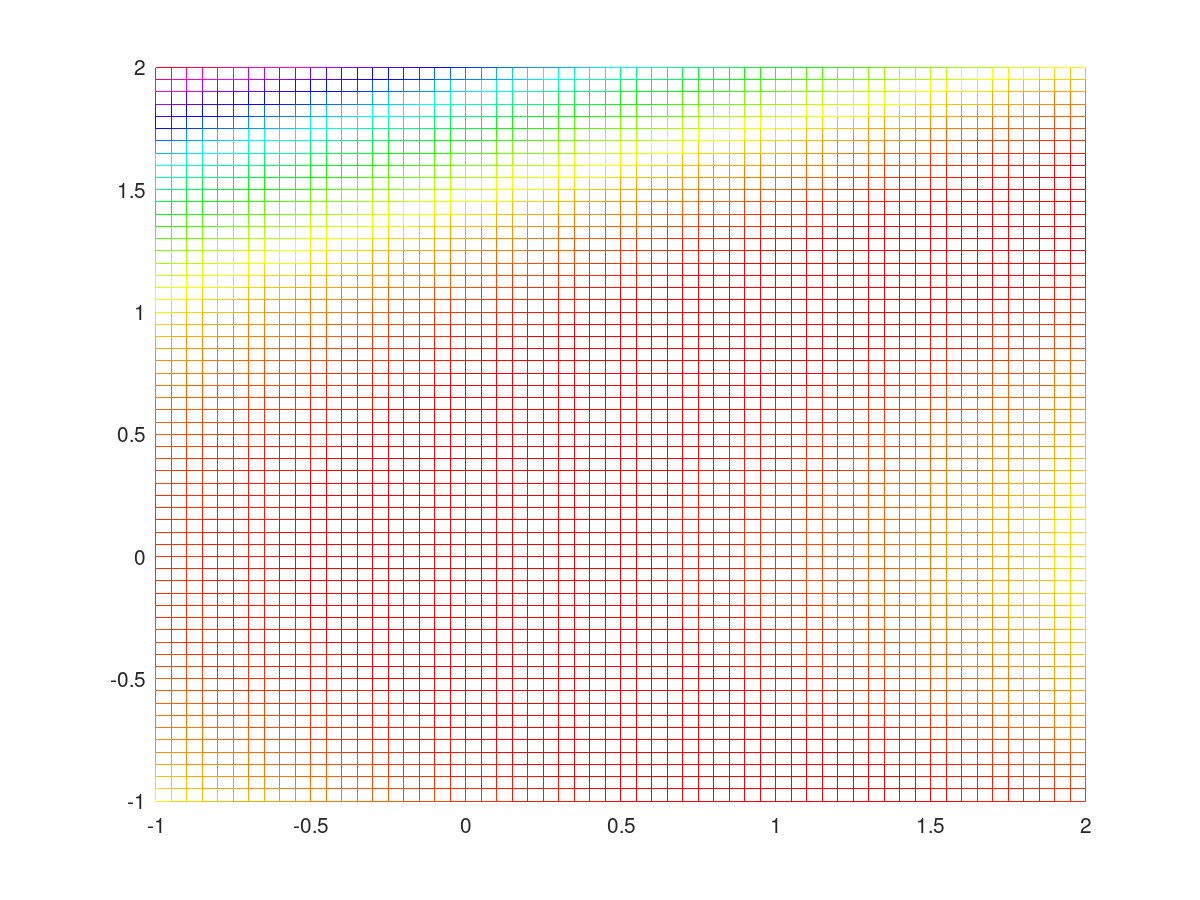
|
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
n = 50
# Create the model
model = mdl.Model("Rosenbrock")
# Create the variables
xs = []
for i in range(n):
xs.append(mdl.Variable(model, f"x_{i}", lb=-5, ub=10))
# Create the objective
expr = mdl.Expression()
for i in range(n-1):
expr += 100 * (xs[i+1] - xs[i]**2)**2 + (1 - xs[i])**2
mdl.Minimize(model, "objective", expr)
# Configure the parameters and environment
parameters = mdl.Parameters(objective_goal=1e-7)
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, parameters, environment)
# Print the solution
print(", ".join(f"{x}: {v:.3f}" for x, v in ans.solution.items()))
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 1592892686195745296a785d5cb959864a475aa0564b8548b
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:26|created: ''
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:27|processing: ''
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:29|partial: 'Objective: 65023.6731758324. Feasibility: 0.0. Iterations: 0. Elapsed: 0.0173900016'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:37|partial: 'Objective: 37.178676752158005. Feasibility: 0.0. Iterations: 52. Elapsed: 10.0258055'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:47|partial: 'Objective: 26.252057701196268. Feasibility: 0.0. Iterations: 103. Elapsed: 20.0318832'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:11:57|partial: 'Objective: 15.497605891001413. Feasibility: 0.0. Iterations: 153. Elapsed: 30.0541039'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:12:07|partial: 'Objective: 5.645950043876712. Feasibility: 0.0. Iterations: 196. Elapsed: 40.134243'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:12:17|partial: 'Objective: 0.019586669729852332. Feasibility: 0.0. Iterations: 240. Elapsed: 50.1468544'
INFO:eut.peerless.solver:..|1592892686195745296a785d5cb959864a475aa0564b8548b|20200623T02:12:22|executed: 'Objective: 9.999999990787735e-08. Feasibility: 0.0. Iterations: 253. Elapsed: 52.9871979'
x_0: 1.000, x_1: 1.000, x_2: 1.000, x_3: 1.000, x_4: 1.000, x_5: 1.000, x_6: 1.000, x_7: 1.000, x_8: 1.000, x_9: 1.000, x_10: 1.000, x_11: 1.000, x_12: 1.000, x_13: 1.000, x_14: 1.000, x_15: 1.000, x_16: 1.000, x_17: 1.000, x_18: 1.000, x_19: 1.000, x_20: 1.000, x_21: 1.000, x_22: 1.000, x_23: 1.000, x_24: 1.000, x_25: 1.000, x_26: 1.000, x_27: 1.000, x_28: 1.000, x_29: 1.000, x_30: 1.000, x_31: 1.000, x_32: 1.000, x_33: 1.000, x_34: 1.000, x_35: 1.000, x_36: 1.000, x_37: 1.000, x_38: 1.000, x_39: 1.000, x_40: 1.000, x_41: 1.000, x_42: 1.000, x_43: 1.000, x_44: 1.000, x_45: 1.000, x_46: 1.000, x_47: 1.000, x_48: 1.000, x_49: 1.000
Notice that in this case, partial solutions are reported and
eut.peerless.model.Expression is used to build an expression for
the objective function.
Constrained mixed-integer nonlinear¶
Hock & Schittkowski problem 62
In this example it is shown how to add an equality constraint and the use
of the eut.peerless.model.log function.
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
# Create the model
model = mdl.Model("HS62")
# Add the variables
x1 = mdl.Variable(model, "x1", 0, 1)
x2 = mdl.Variable(model, "x2", 0, 1)
x3 = mdl.Variable(model, "x3", 0 ,1)
# Add the objective function
mdl.Minimize(model, "objective",
-32.174 *
(255*mdl.log((x1 + x2 + x3 + 0.03)/ (0.09*x1 + x2 + x3 + 0.03)) +
280*mdl.log((x2 + x3 + 0.03)/(0.07*x2 + x3 + 0.03)) +
290*mdl.log((x3 + 0.03)/(0.13*x3 + 0.03))))
# Add the constraints
model.add_constraint(x1 + x2 + x3 == 1, "ct1")
# Configure the parameters and environment
parameters = mdl.Parameters()
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, parameters, environment)
# Print the solution
print(ans.solution)
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 159300142726341324949b0eb66418f08fe1cc59433089335
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|159300142726341324949b0eb66418f08fe1cc59433089335|20200624T08:23:47|created: ''
INFO:eut.peerless.solver:..|159300142726341324949b0eb66418f08fe1cc59433089335|20200624T08:23:48|processing: ''
INFO:eut.peerless.solver:..|159300142726341324949b0eb66418f08fe1cc59433089335|20200624T08:23:50|executed: 'Objective: -26268.801021928404. Feasibility: 1.6935983726540371e-09. Iterations: 304. Elapsed: 0.436048001'
{x1: 0.6201304283392307, x2: 0.32229642390764984, x3: 0.057573149446717674}
TLN2 from MINLPLib
This nonlinear example has three binary variables, six integer variables and twelve inequality constraints.
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
# Create the model
model = mdl.Model("TLN2")
# Add the variables
b1 = mdl.BinaryVariable(model, "b1")
b2 = mdl.BinaryVariable(model, "b2")
b3 = mdl.BinaryVariable(model, "b3")
i3 = mdl.IntegerVariable(model, "i3", lb=0, ub=15)
i4 = mdl.IntegerVariable(model, "i4", lb=0, ub=15)
i5 = mdl.IntegerVariable(model, "i5", lb=0, ub=5)
i6 = mdl.IntegerVariable(model, "i6", lb=0, ub=5)
i7 = mdl.IntegerVariable(model, "i7", lb=0, ub=5)
i8 = mdl.IntegerVariable(model, "i8", lb=0, ub=5)
# Add the objective function
mdl.Minimize(model, "objective", 0.1 * b1 + 0.2 * b2 + i3 + i4)
# Add the constraints
model.add_constraint(460 * i5 + 570 * i7 <= 1900, "ct1")
model.add_constraint(460 * i6 + 570 * i8 <= 1900, "ct2")
model.add_constraint(460 * i5 + 570 * i7 >= 1700, "ct3")
model.add_constraint(460 * i6 + 570 * i8 >= 1700, "ct4")
model.add_constraint(i5 + i7 <= 5, "ct5")
model.add_constraint(i6 + i8 <= 5, "ct6")
model.add_constraint(b1 - i3 <= 0, "ct7")
model.add_constraint(b2 - i4 <= 0, "ct8")
model.add_constraint(i3 <= 15 * b1, "ct9")
model.add_constraint(i4 <= 15 * b2, "ct10")
model.add_constraint(i3 * i5 + i4 * i6 >= 8, "ct11")
model.add_constraint(i3 * i7 + i4 * i8 >= 7, "ct12")
# Configure the parameters and environment
parameters = mdl.Parameters()
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, parameters, environment)
# Print the solution
print(ans.solution)
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 15930142453220828406514fd3fc2c4ed5751e17d71852289
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|15930142453220828406514fd3fc2c4ed5751e17d71852289|20200624T11:57:25|created: ''
INFO:eut.peerless.solver:..|15930142453220828406514fd3fc2c4ed5751e17d71852289|20200624T11:57:26|processing: ''
INFO:eut.peerless.solver:..|15930142453220828406514fd3fc2c4ed5751e17d71852289|20200624T11:57:29|executed: 'Objective: 5.3. Feasibility: 0.0. Iterations: 58. Elapsed: 0.323506981'
{b1: 1.0, b2: 1.0, b3: 1.0, i3: 3.0, i4: 2.0, i5: 0.0, i6: 4.0, i7: 3.0, i8: 0.0}
NVS08 from MINLPLib
This is another example with two integer variables, one continuous variable and
three inequality constraints, using the eut.peerless.model.sqrt
function.
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
# Create the model
model = mdl.Model("NVS08")
# Add the variables
i1 = mdl.IntegerVariable(model, "i1", lb=0, ub=200)
i2 = mdl.IntegerVariable(model, "i2", lb=0, ub=200)
x3 = mdl.Variable(model, "x3", lb=0.001, ub=200)
# Add the objective function
mdl.Minimize(model, "objective", (-3 + i1)**2 + (-2 + i2)**2 + (4 + x3)**2)
# Add the constraints
model.add_constraint(mdl.sqrt(x3) + i1 + 2 * i2 >= 10, "ct1")
model.add_constraint(0.240038406144983 * i1**2 - i2 + 0.255036980362153*x3
>= -3, "ct2")
model.add_constraint(i2**2 - 1 / (x3**3 * mdl.sqrt(x3)) - 4*i1 >= -12, "ct3")
# Configure the parameters and environment
parameters = mdl.Parameters()
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, parameters, environment)
# Print the solution
print(ans.solution)
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 15930057417047899ddb985a042d85104af66626f167871a
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|15930057417047899ddb985a042d85104af66626f167871a|20200624T09:35:41|created: ''
INFO:eut.peerless.solver:..|15930057417047899ddb985a042d85104af66626f167871a|20200624T09:35:43|acquired: ''
INFO:eut.peerless.solver:..|15930057417047899ddb985a042d85104af66626f167871a|20200624T09:35:45|executed: 'Objective: 23.449727345986304. Feasibility: 4.8259174434406304e-09. Iterations: 63. Elapsed: 0.296331018'
{i1: 4.0, i2: 3.0, x3: 0.6313850353848042}
Mixed-integer linear programming¶
MIP’s have a particular structure for which there exists very efficient algorithms that can solve problems with millions of variables and constraints. In case the problem is a MIP, Peerless uses one of these specialized algorithms to achieve the best possible performance.
The Unit Commitement Problem
In this very simplified version of the Unit Commitment problem, we’re looking for an operation plan of electric generators such that demand, \(d_t\), is satisfied for all hours, \(t=1,\ldots,n\), and cost is minimized.
Every time a unit, \(i\), starts or shuts down, a startup cost, \(s_i\), or shutdown cost, \(r_i\), are incurred. Also, units can only operate between their minimum, \(p_i^{min}\), and maximum power, \(p_i^{max}\).
Given \(m\) units, \(\forall i=1,\ldots,m,t=1,\ldots,n\), define the following variables:
\(u_{i,t}\in\{0,1\}\): indicating if unit \(i\) is on at time \(t\).
\(v_{i,t}\in\{0,1\}\): indicating if unit \(i\) starts at time \(t\).
\(w_{i,t}\in\{0,1\}\): indicating if unit \(i\) shuts down at time \(t\).
\(p_{i,t}\in\{0\}\cup[p_i^{min},p_i^{max}]\): is the operating power of unit \(i\) at time \(t\).
The problem can be stated as follows:
import collections
import logging
logging.basicConfig(level=logging.DEBUG)
import eut.peerless.model as mdl
import eut.peerless.solver as solver
class Unit:
def __init__(self, name, startup_cost, shutdown_cost, pmin, pmax):
self.name = name
self.startup_cost = startup_cost
self.shutdown_cost = shutdown_cost
self.pmin = pmin
self.pmax = pmax
# Create the model
model = mdl.Model("Unit Commitment")
# Define the number of hours
nb_hours = 24
# Create the units
units = [Unit("U1", 10000, 1500, 100, 500),
Unit("U2", 12000, 1550, 200, 600),
Unit("U3", 14000, 1560, 150, 450)]
# Create the demand
demand = [600, 700, 800, 900, 920, 930,
930, 920, 900, 800, 700, 600,
500, 450, 400, 350, 300, 200,
150, 140, 150, 200, 400, 500]
# Create the variables
u = collections.defaultdict(list)
v = collections.defaultdict(list)
w = collections.defaultdict(list)
p = collections.defaultdict(list)
for unit in units:
for t in range(nb_hours):
u[unit].append(mdl.BinaryVariable(model, f"u_{unit.name}-{t}"))
v[unit].append(mdl.BinaryVariable(model, f"v_{unit.name}-{t}"))
w[unit].append(mdl.BinaryVariable(model, f"w_{unit.name}-{t}"))
p[unit].append(mdl.Variable(model, f"p_{unit.name}-{t}",
lb=0, ub=unit.pmax))
# Create the commitment constraints
# u[t] - u[t-1] == v[t] - w[t]
for unit in units:
# Units are off before the beginning of the period
model.add_constraint(u[unit][0] - 0 == v[unit][0] - w[unit][0])
# The rest of the periods
for t in range(1, nb_hours):
model.add_constraint(u[unit][t] - u[unit][t-1] ==
v[unit][t] - w[unit][t])
# Create the power bounds constraints
for unit in units:
for t in range(nb_hours):
# pmin * u <= p <= pmax * u
model.add_constraint(unit.pmin * u[unit][t] <= p[unit][t])
model.add_constraint(p[unit][t] <= unit.pmax * u[unit][t])
# Create the demand constraint
for t in range(nb_hours):
# sum(unit) p == demand
expr = mdl.Expression()
for unit in units:
expr += p[unit][t]
model.add_constraint(expr == demand[t])
# Create the objective function: sum(unit) startup + shutdown
objective_expr = mdl.Expression()
for unit in units:
for t in range(nb_hours):
objective_expr += unit.startup_cost * v[unit][t]
objective_expr += unit.shutdown_cost * w[unit][t]
mdl.Minimize(model, "obj", objective_expr)
# Configure the environment
environment = solver.Environment("your@email.com", "password")
# Solve the model
ans = solver.solve(model, mdl.Parameters(), environment)
# Print the solution
for unit in units:
print(f"{unit.name:8s}:", end="")
for t in range(nb_hours):
variable = p[unit][t]
print(f"{ans.solution[variable]:8.2f}", end=" ")
print()
print("Demand :", end="")
for t in range(nb_hours):
print(f"{demand[t]:8.2f}", end=" ")
print()
INFO:eut.peerless.solver:Sending problem to the jobstore
INFO:eut.peerless.solver:..job's key is 15943793068768666553806d186824e93ff14241429fc6d39
INFO:eut.peerless.solver:..pooling every 2 seconds
INFO:eut.peerless.solver:..|15943793068768666553806d186824e93ff14241429fc6d39|20200710T07:08:26|created: ''
INFO:eut.peerless.solver:..|15943793068768666553806d186824e93ff14241429fc6d39|20200710T07:08:27|processing: ''
INFO:eut.peerless.solver:..|15943793068768666553806d186824e93ff14241429fc6d39|20200710T07:08:29|executed: 'Objective: 23550.0. Feasibility: 0.0. Iterations: None. Elapsed: 2.0737478733062744'
U1 : 400.00 500.00 500.00 500.00 500.00 500.00 500.00 500.00 500.00 500.00 500.00 400.00 300.00 250.00 200.00 350.00 300.00 200.00 150.00 140.00 150.00 200.00 400.00 500.00
U2 : 200.00 200.00 300.00 400.00 420.00 430.00 430.00 420.00 400.00 300.00 200.00 200.00 200.00 200.00 200.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
U3 : 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Demand : 600.00 700.00 800.00 900.00 920.00 930.00 930.00 920.00 900.00 800.00 700.00 600.00 500.00 450.00 400.00 350.00 300.00 200.00 150.00 140.00 150.00 200.00 400.00 500.00